• Точка та пряма
• Дві прямі
• Пряма та площина, точка та площина

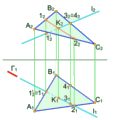
     Пряма належить площині, якщо дві її точки належать цій площині (рис. 3.4,а) або, коли вона проходить через точку, що належить площині, та паралельна іншій прямій, що належить даній площині ( рис. 3.4,б ).

Рис. 3.4

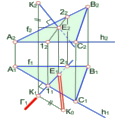
     Лінія рівня належить площині, якщо дві її точки належать цій площині та вона є паралельною одній з площин проекцій. Так на рис. 3.5 зображено горизонталь h, яка належить площині Q(CAВ) та паралельна – П1.

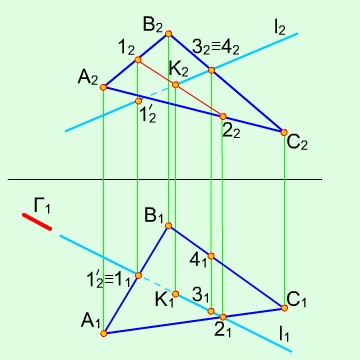
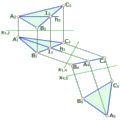
     Пряма може перетинати площину або бути їй паралельною, тобто перетинати в невласній точці – перша основна позиційна задача. Розглянемо перетин прямої з площиною (рис. 3.6). Для визначення точки перетину прямої з площиною доцільно застосовувати допоміжну площину, яка проходить через пряму і є проекціюючою по відношенню до однієї з площин проекції. Для цього через пряму проводять допоміжну прекціюючу площину, наприклад, горизонтально – проекціюючу площину Г та знаходять лінію перетину двох площин – пряму 1-2 (її горизонтальну проекцію 1121), за горизонтальною проекцією визначено фронтальну проекцію 1222. У перетині проекції l2 прямої та проекції 1222 лінії перетину знайдемо шукану точку К2 – перетин прямої з площиною. Видимість відрізків прямої l визначається за допомогою конкуруючих точок 3 і 4.

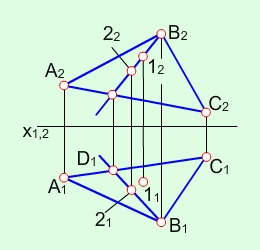
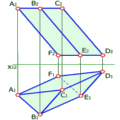
     Точка може належати площині або не належати їй. Це визначається за допомогою прямої, що належить площині (рис. 3.7).

Рис. 3.5

Рис. 3.6

Рис. 3.7

 

Дві площини
• Перелік тем